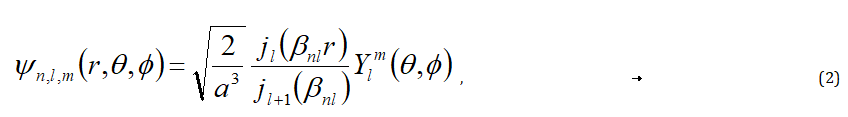¹Centro de Nanociencias y Nanotecnología, Universidad Nacional Autónoma de México, México

²IPCM-Ciência dos Materiais, Universidade Federal do Vale do São Francisco, 48902-300 Juazeiro, BA, Brazil

*Corresponding author: Mufei Xiao, Centro de Nanociencias y Nanotecnología, Universidad Nacional Autónoma de México, km. 107 Carretera Tijuana-Ensenada, Ensenada, Baja California CP 22860, México; Email: [email protected]

Received Date: March 31, 2023

Publication Date: April 24, 2023

Citation: Xiao M, et al. (2023). Nondestructive Sizing of Quantum Particles (1 ~ 3 nm) Via Quantum-Size and Temperature-Induced Plasmon Shift. Catalysis Research. 3(2):11.

Copyright: Xiao M, et al. © (2023). 

ABSTRACT

It is proposed a method to non-destructively determine the size (1~3 nm) of metallic particles doped in otherwise optically transparent materials, based on a theoretical study on the plasmonic shift induced by the quantum-size effect and the environmental temperature. It is of recent interest to study plasmonics of metallic particles that are so small that carriers in the conduction band are separated at discrete subbands due to quantum confinement. These small metallic particles are referred to as quantum particles in the present work. The modifications of the plasmons of the quantum particles are studied with an every-electron-count computational scheme. The quantum size effects are incorporated into classic descriptions of small particle plasmons with an emphasis on intra-subband fluctuations caused by quantum confinement. The carrier redistribution at the subbands is related to the operational temperature via Fermi-Dirac expression. Numerical results have shown that both the frequency and the strength of the plasmons are modified as a function of the particle size and the operational temperature. The discovery suggests potential applications, such as tuning the plasmonics of quantum particles externally and nondestructive sizing of the particles 1~3 nm in size. The environment temperature can be conveniently controlled by light, electricity, or other means.

Keywords: Plasmonics, quantum particles, quantum-size effect, Fermi-Dirac distribution, nondestructive sizing

INTRODUCTION

Recently small metallic particle doping materials are widely used for various purposes. Here is an example. Zeolites are crystalline microporous aluminosilicates that have found wide-ranging industrial applications in catalysis as well as in other processes. An effective way to enhance the chemistry processes is to inject plasmonic nanostructures and particles [1-4]. Particles of noble metals, such as silver and gold, are excellent plasmonic media. Surface plasmons and small particle plasmons may be excited by light [5-7]. The enhanced optical reactions stem from the collective resonances due to doping metallic particles in zeolite materials. The doping appears helpful for increasing catalytic efficiency and zeolite harvest.

Plasmonics of small metallic particles were extensively studied in the past [8-10]. Plasmons of small metallic particles can be experimentally observed with high-resolution optical spectroscopy in the far field or scanning near-field optical microscopy in the near field, and the changes in plasmon frequency and strength are indications for analyzing particle properties as well as the properties of surrounding objects.

Plasmon excitation of small metallic particles has been shown useful in various applications in photonic, biological, and medical studies. On the other hand, the understanding of dipolar radiation associated with the plasmon excitation of a single metallic particle is often adopted in studying more complicated nanostructures [6-12].

With the rapid development in nanometric sciences and technologies, a recent trend in the study of small metallic particles is to reduce the particle size so that carriers in the conduction band bear energies at discrete subbands due to quantum confinement [13]. For the quantum size effects to be significantly manifested, the size of the particles has to be small enough within a few nanometers.

Therefore, it becomes desired to develop a theory and a feasible computational scheme to relate the quantum size effects to the plasmon excitation of quantum particles. Indeed, the present author showed in the past a workable scheme to deal with the problem in the assumption that the particles are placed in an environment where the temperature is kept low enough [14]. Considering the current experimental studies on this subject, it appears highly desirable to extend the theory to take into account temperature changes, which is the aim of the present work.

The temperature dependence can be incorporated into the theory via the Fermi-Dirac distribution of the carriers at different subbands [15,16]. The redistributed carrier density becomes a function of the temperature, so as do the plasmonic behaviors of the quantum particles. The observed temperature dependence of the plasmons of quantum particles suggests potential applications to externally control the plasmons of the quantum particles, which provides useful guidance for further experimental studies in this research direction.

In the present work, we pay attention to the relationship between environmental temperature and particle size. We propose a nondestructive sizing method for nanoparticles 1 ~ 3 nm in size by observing the plasmon shift due to a change of temperature with a high-resolution optical spectroscope. The paper is organized as follows. In Section 1, the theory is outlined. In Section 2, some numerical results are presented and the results are discussed. Finally, the work is concluded in Section 3.

FORMALISM

In this Section, we outline formalism for numerical calculations. More details of the theory can be found in Ref. [15,16]. In passing, we take two important notes as follows. In the present work, we shall not consider inter-subband transitions. One can handle the intra- and inter-subband transitions separately because the two frequency ranges usually not to be overlapped each other [14]. It is also well-known that the damping effects are modified when the particle size is reduced. However, in the present work, a constant number is used for the damping factor, which is to avoid having extra parameters simultaneously in the computation, so that the changes in plasmon frequency due to quantum size effects and temperature could be emphasized. Indeed, the damping factor changes mainly the shape of the plasmon peaks and has less impact on the location of the plasmon frequency.

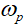
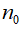
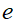
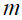
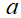
Plasmon exists in all conducting media including plasmas and metals, its angular frequency  can be calculated from , where  is the carrier density,  and  the charge and mass of the carrier respectively, and  the permittivity of free space. It is well known that bulk plasmon cannot be excited by light. Surface plasmon at a metal-dielectric interface can however be excited with prism, grating, fiber tip, etc. For small metallic particles, surface plasmons exist also at the boundary. Since the particle is small, the surface plasmon polaritons are highly localized, and therefore surface plasmons of small particles are often referred to as the localized plasmon. However, for quantum particles that are studied in the present work, since the size is dramatically reduced, it is unlikely that this kind of surface plasmon could be excited. Instead, the small particle plasmon can be excited, which can be observed in the Rayleigh polarizability for small spherical particles of radius  as

 

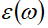
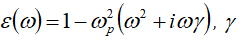
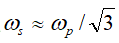
where the relative dielectric function  can be calculated from the plasmon frequency according to the Drude model ,  being a damping factor. Substituting the Drude expression into Eq. 1, one realizes that the maximum absorption and also the strongest scattering happens when , which can be referred to as the small particle plasmon frequency.

However, if the uniform electron density is replaced by a position-dependent density due to a variant dielectric function, the polarizability of the particle becomes integral over the particle volume. The modification of the electron density is caused by quantum confinement. Therefore, the next task is to calculate the carrier distribution with a quantum mechanics model. In the electron-in-a-box model, one writes down the wave functions for spherical particles as

 

 

where  is the spherical Bessel function with the zero points  and the spherical harmonics are composed with Legendre polynomials . The energy corresponding to the wave function can be determined by , and the electrons occupy the discrete energy levels according to the Fermi-Dirac distribution

 

 

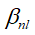
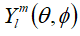
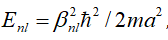
where  is the Fermi energy,  is the Boltzmann constant, and  the temperature.

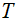
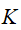
So far, we have listed the necessary mathematical expressions for computation. The computational task is usually heavy as it may involve a very large number of electrons. A common practice in the literature in treating a large number of carriers is to find some sum rules so that the summation can be converted into integrals. However, in the process, the information about the quantum confinement may be overlooked or modified, so that the results would be less reliable for particles where the number of carriers is not that big. In the present work, we adopt a computational scheme that accounts for every electron. Since the particles we are interested in are rather small, we have successfully handled the computation on a supercomputer [15,16].

RESULTS AND DISCUSSIONS

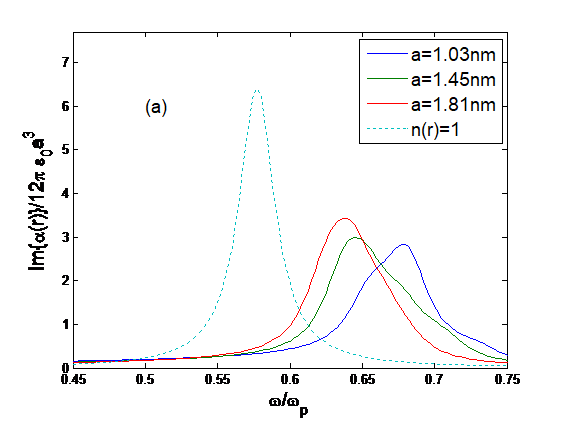
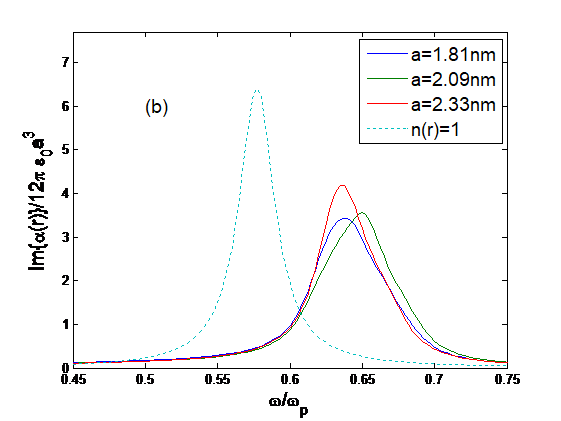
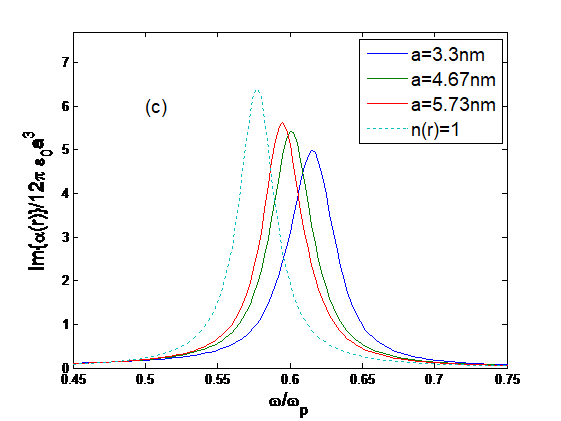
Let us present some numerical results obtained from the above-listed formalism. First, we present some results similar to those in Ref. [15] to show how the plasmon is shifted with the quantum-size effect and temperature. The reference for the plasmon is the standard Gaussian peak for Raylagh particles, i.e., the quantum size effects are not considered. The spectrum is normalized to the peak frequency, i.e., the plasmon. Since the theory is universally useful for all conducting materials, the selection of actual plasmon frequency is conserved. Note that for a material with a plasmon frequency of 500 nm, a shift of 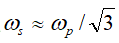 means 5 nm. Modern high-resolution optical microscopes can easily pick up frequency shifts of < 0.1 nm.

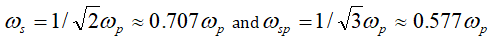
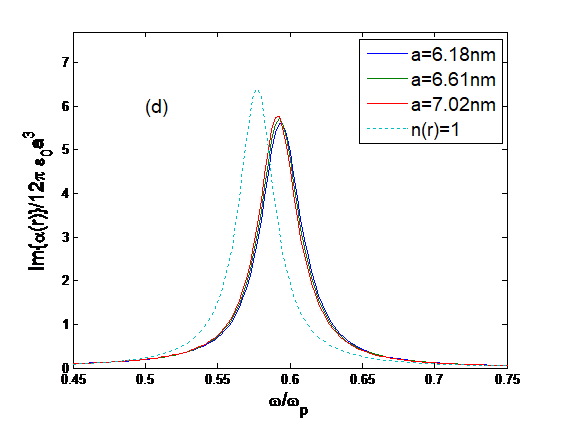
Note that if both the quantum size effect and the temperature effect are not considered, the surface plasmon and the small-particle plasmon appear at  and , respectively. In our case, we should make use of the small-particle plasmon. When the quantum size effect is considered, the plasmon shifts with the decrease of the particle size. The quantum size effect becomes significant only when the particle size is reduced to about a few nanometers. Further reducing the particle size to less than say 1 nm, the plasmon is less reliable, and inter-band transits would be dominating. We show in Figure 1 the situation we described here. Particle size is reduced from 7 to 1 nm in four sub-figures. One sees that when the particle size is larger than 4 nm, the plasmon shift appears not significant and the shift becomes significant in 1 ~ 3 nm. When the particle size is reduced to less than 1 nm, the theory is less reliable, as there are not many electrons in the particle, and the plasmon appears complex and weak.

Figure 1: Normalized imaginary part of polarizability as a function of normalized angular frequency.

 for various radii: (a) a = 1.03, 1.45, 1.81 nm; (b) a = 1.81, 2.09, 2.33 nm; (c) a = 3.30, 4.67,

5.73 nm and (d) a = 6.18, 6.61, 7.02 nm at T = 0. The dotted line is for n(r) = 1.

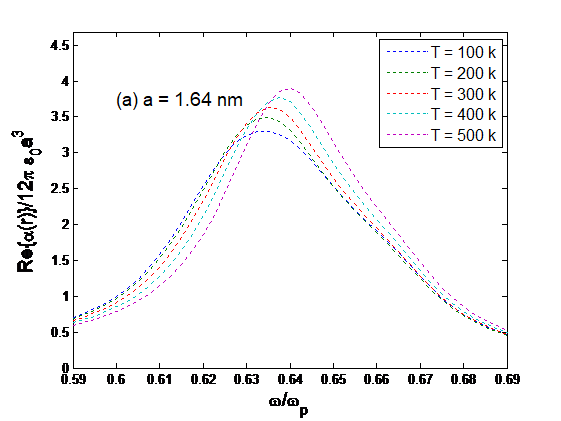
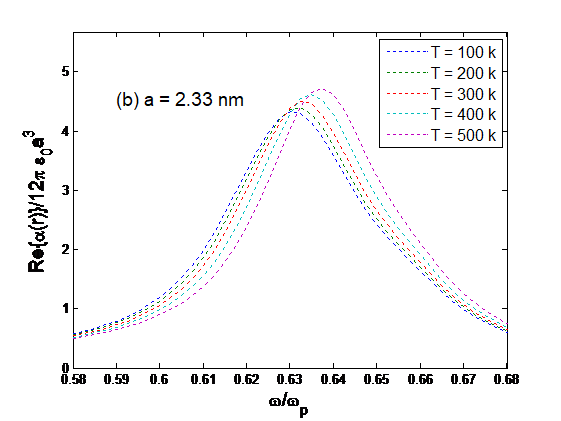
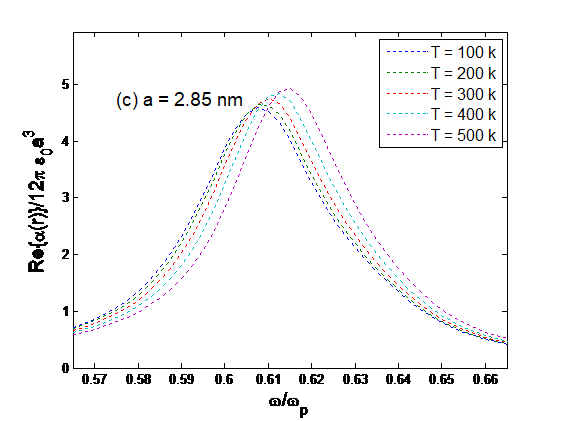
We then apply the temperature effect to the plasmon shift, in addition to the quantum size effect shown in Figure 1. Note also that both the quantum size effect and the temperature effect occur simultaneously. In the numerical calculations, the two effects are treated in two steps, to show the changes brought up by each effect. In Figure 2, the imaginary parts of the polarizability of the four particles of different sizes are presented with various temperatures. It is demonstrated that both the strength and the frequency of the small-particle plasmon vary with the size and the temperature, and the modifications are more significant for smaller particles.

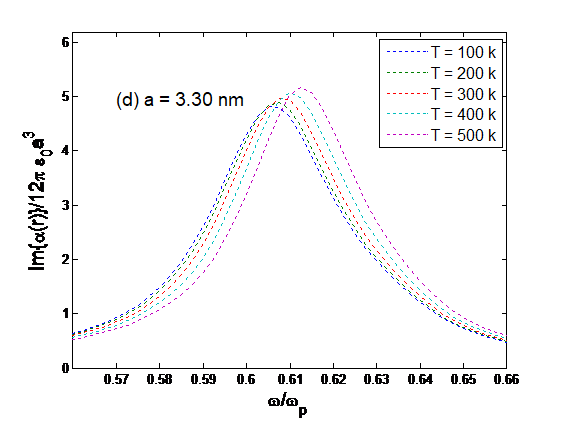
Figure 2: Normalized imaginary part of polarizability as a function of normalized angular frequency for various radii: (a) a=1.64 nm; (b) a=2.33 nm; (c) a=2.85 nm; (d) a=3.30 nm at various temperatures: T=100k, 200k, 300k, 400k, 500k.

In Figure 2, the temperature dependence of the strength and frequency of small-particle plasmon is presented for particles of different sizes. In general, the change in frequency increases with the increase in temperature, and the plasmon strength is reduced for smaller particles. As one may expect, the temperature dependence is not straightly linear. It appears that in some temperature ranges, the changes in plasmon frequency and strength can be more significant than in other temperature ranges.

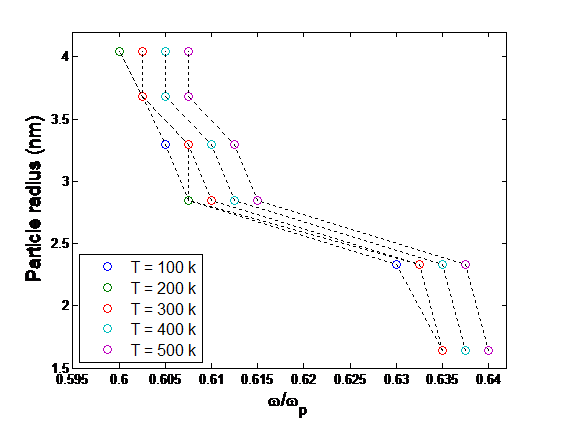
Let us now pay attention to the relationship between the particle size and the quantum-size effect plus temperature-induced plasmon shift. It is complicated to present three-variable figures and tables. We choose to present the data as in Figure 3， where particle size is related to the plasmon shift for various temperatures.

Figure 3: Particle radius as a function of plasmon shift , at various temperatures: T=100k, 200k, 300k, 400k, 500k.

One may see in Figure 3 that both the quantum-size effect and temperature-induced plasmon shift may be used to measure the particle size. The best range of sizing is about 1 ~3 nm. For larger particles, the quantum-size effect becomes insignificant, whereas, for smaller particles, the plasmon spectrum appears complicated and weak. Note also that the y-axis in Figure 3 represents the particle size, which is different from the previously presented [15] plasmon strength dependence. The curves look similar but not the same thing. Plasmon strength is hard to value as there may be influences from various sources. As one can see in Figure 3, the required resolution for the spectroscopy would be 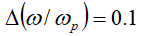, which corresponds to a few nanometers for a plasmon in visible. One also realizes that low temperature and vacuum environment are unnecessary, and even the temperature would be used for estimating the particle size.

CONCLUSIONS

In the present work, it has been demonstrated that the small-particle plasmon of metallic particles is size and temperature dependent due to quantum confinement. The quantum effects can be significant for metallic particles of a few nanometers. This modification stems from the quantum size effects and is apart from the usually well-known size effects within classic descriptions. However, the modification of plasmons with changing particle sizes can hardly be implemented when the samples are already prepared. Based on the numerical results, one sees the opportunities to tune the plasmon (frequency and strength) of small metallic particles. An apparent opportunity is to assert the size of the nanoparticles embedded in optically transparent materials. Optical spectroscopy with a resolution of a few nanometers may carry out the work. Low temperature and vacuum environments are not necessary. In addition, the proposed method is useful to assert the samples, for judgment on if the samples contain metallic particles in the size range and if the dominant optical response comes from a small-particle plasmon regime. One of the possible applications of the proposed method is to estimate the size of metallic particles embedded in zeolite materials. Relevant experimental results will be included in our forthcoming publications.

ACKNOWLEDGMENT

This work was supported by PAPIIT-UNAM under Project IN100514 and the supercomputer at UNAM.

REFERENCES

1. Zhang X, Ke X, Du A, Zhu H. (2014). Plasmonic nanostructures to enhance catalytic performance of zeolites under visible light. Sci Rep. 4:3805.
2. Linic S, Christopher P, Ingram D. (2011). Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy. Nat Mater. 10:911–921.
3. Maier A, et al. (2001). Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides. Nat Mater. 2:229–232.
4. Wang F, Li C, Chen H, Jiang R, Sun L, Quan Li, et al. (2013). Plasmonic harvesting of light energy for Suzuki coupling reactions. J Am Chem Soc. 135:5588–5601.
5. Xiao M, Bozhevolnyi S. (2001). Resonant field enhancement by a finite-size periodic array of surface scatterers. J Phys Condens Matter. 13:3001.
6. Xiao M. (1997). Theoretical treatment for scattering scanning near-field optical microscopy. J Opt Soc Am A. 14:2977-2984.
7. Xiao M, Zayats A, Siqueiros J. (1997). Scattering of surface-plasmon polaritons by dipoles near a surface: Optical near-field localization. Phys Rev B. 55:1824-1937.
8. Genzel L, Martin T, Kreibig U. (1975). Dielectric function and plasma resonances of small metal particles. Z Phys B. 21:339-346.
9. Willets K, Van Duyne R: (2007). Localized surface plasmon resonance spectroscopy and sensing. Annu Rev Phys Chem. 267:267-297.
10. Novo C, Funston A, Mulvaney P. (2008). Direct observation of chemical reactions on single gold nanocrystals using surface plasmon spectroscopy. Nature Nanotechnol. 3:598-602.
11. Lal S, Clare S, Halas N. (2008). Nanoshell-enabled photothermal cancer therapy: impending clinical impact. Acc Chem Res. 41:1842-1851.
12. Butet J, Thyagarajan K, Martin O. (2013). Ultrasensitive Optical Shape Characterization of Gold Nanoantennas Using Second Harmonic Generation. Nano Lett. 13:1787-1792.
13. Scholl J, Koh A, Dionne J. (2012). Quantum plasmon resonances of individual metallic nanoparticles. Nature. 483:421-427.
14. Xiao M. (2001). Competing intra- and inter-band transitions in quantum dots as manifested in optical absorption spectra. Phys Lett A. 288:37-40.
15. Xiao M, Rakov N. (2015). Size and temperature dependent plasmons of quantum particles. Int J Mod Phys B. 29:1550146.
16. Xiao M. (2020). Fine tuning of quantum particle plasmon. Optik. 216:164866.